Design tidal turbine or wind turbine software heliciel
tidal turbine, windmills, wind turbine, hydroelectric turbines: "energy harvesting"
| The energy available | The energy that we can capture | wind turbines | tidal turbines | hydroelectric turbines |
Understand and master the tidal turbine, windmills, wind turbine and hydroelectric turbines:
Capture the energy of fluid streams with a propeller system is encountered in many systems of energy production and driving force.
The characteristics of the sensed fluid, air or water, changing some constraints, but the principle of energy conversion remains the same. So before going deeper into the wind turbines, tidal turbines or hydro turbines, we will take stock of this method of energy conversion.Before to engage in the design of the propeller, We must assess the need for energy and compare it to the energy available on the site of implantation.Energy from fluid is kinetic energy. The kinetic energy is the energy of the velocity of an object.
- eq1: E(joule)= 0.5 X mass (Kg) X velocity²(m/sec)
- eq2: mass(Kg)=density(kg/m3) X propeller disk area(m²) X velocity (m/sec)
- equ3:P(W)=0.5 X density(kg/m3) X(velocity)³ (m/sec) X disk area(m²) .
We notice that power is a cubic function of the speed: if the speed is doubled, the power multiplies by eight!The disc surface swept by the propeller is the best indicator of its potential:
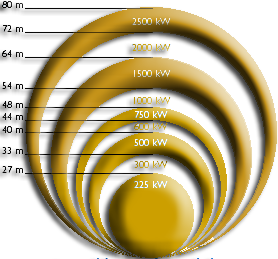
The energy that we can capture:
Any energy transformation involves loss.
The essential first loss, due to the fact that to get all the power of the fluid velocity, it would have to remove all its speed as it passes through the propeller. if it stops all fluid entering the impeller, where it puts? It's got to be evacuated from the other side the propeller and this quickly enough to leave space for the incoming air ! So we can use that a part of the power of the fluid stream. More propeller removed from the fluid velocity, the more it slows down the passage and the fluid loses its energy without transmitting it to our propeller ..For a more mathematical explanation theory froude using the concept of momentum can be foundBetween the case where no speed to the fluid, and where it prevents the passage is removed, there is a case where the maximum possible energy of the fluid is extracted. This ideal case, corresponds to a reduction of the fluid velocity of 1/3 of its speed upstream.The maximum recoverable energy (calculated and shown by Betz) is 16/27 to energy of the fluid. This is the Betz limit:
- equ4: Pmax(W)=16/27 X 0.5 X density(kg/m3) X velocity³ (m/sec) X disk area (m²) .
- equ5_A: Pmax(W)=0.37 X (disk area m²) X wind_speed m/sec)³
For water density 1000 kg/m3 this gives us:The efficiency of an energy transformation can be measured by power before transformation / power after transformation.Our propeller will turn the power of the fluid in power to the propeller shaft. The quality of our propeller will be revealed by the power coefficient (Cp) calculated as follows:
- equ5_B:Pmax(W)=296 X (disk area m²) X (water_speed m/sec)³
- equ6: Cp=shaft_power_w / (0.5 X density_m3_kg X fluid_speed_ms³ X disk_area_m2)
theoretical Cp max announced by Betz, ignores losses due to drag and losses at the blade tip. It results from these losses, that the propellers do not exceed 70_80% of the Betz limit. This reduces our max Cp hoped to 0.4_0.5The surface and the blade length to to give to our propeller can be found to provide the desired power if the wind speed is known and the estimated performance (Cp) :
- equ7: disk_area_m2=shaft_power_w/(Cp X 0.5 X density_m3_kg X fluid_velocity_ms³ )
- equ8: blade length =sqrt((shaft_power_w/(Cp X 0.5 X density_m3_kg X fluid_velocity_ms³ ) ) / 3.14 ) .
- equ8: blade length=sqrt((shaft_power_w/( 0.2 X density_m3_kg X fluid_velocity_ms³ ) ) / 3.14 ) .




 Global site map
Global site map Mecaflux
Mecaflux Tutorials Mecaflux Pro3D
Tutorials Mecaflux Pro3D Tutorials Heliciel
Tutorials Heliciel Mecaflux Store
Mecaflux Store Compare software functions
Compare software functions Quotes, Orders, Payment Methods
Quotes, Orders, Payment Methods project technical studies
project technical studies