
airfoils blade profile
| Optimize the shape of the profiles |
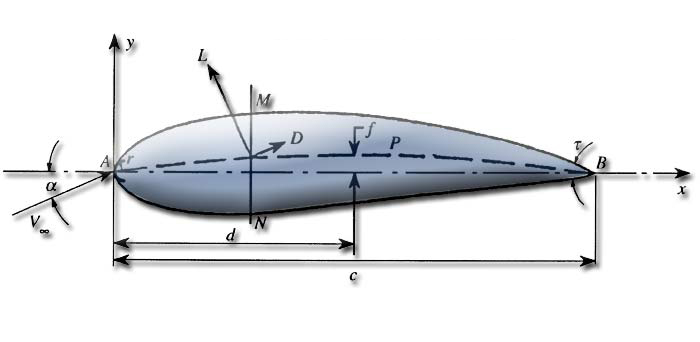
Reminder on the profile geometry:
The profile shape of the wings or blades determine their aerodynamic or hydrodynamic performance but also their mechanical strength. The compromise between performance and mechanical strength is at the heart of the problem of the definition and optimization of the geometry of the wing or blade. In the aerodynamic or hydrodynamic point of view, the higher the profile is fine unless it generates a resistance to the advancement. A slight bend for lift and our sheet s' flies away effortlessly ...

- L = lift force perpendicular to the displacement of the fluid expressed in newtons
- D = drag force paralelle resistant to fluid displacement expressed in newtons
- a = angle attack (or geometric incidence )
- A = Leading Edge
- C = length of the chord
- B = trailing edge
- d = the maximum position of the profile camber
- AB = String reference profile
- f = maximum camber
- AMB = Extrados
- r = radius of the leading edge
- ANB = Intrados
- APB = camber line profile compared to the speed of the flow, Vinfini
- t. = Angle of the trailing edge
- The mid-perpendicular to the reference chord segments, such MN is called the profile or skeleton mean camber line.
- We denote by f the greatest ordinate of the mean camber line over AB.
- The ratio f / c is said camber on
- the maximum value of the MN segment represents the maximum thickness of the profile, e max
- The expression e max / c = t is the maximum relative thickness. Conventional profiles has a relative thickness of 6 to 20% approximately located at C / 3
- the arch is on the order of 6 to 8% and d / e max varies from 15 to 50%.
- On the same figure shows the aerodynamic forces L (lift) and D (drag).
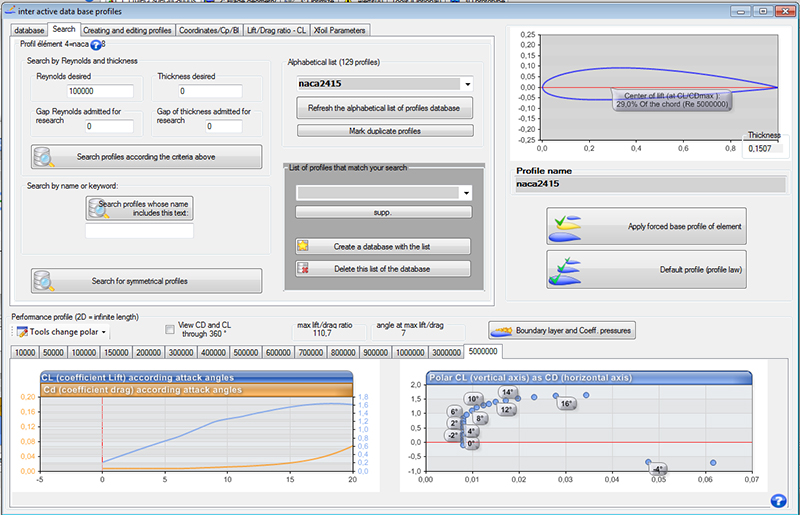
Different types of airfoils are cataloged in the world. Note, for example, Joukowski, Eppler, Wortmann, NACA, RAE, Göttingen, NLR, NASA / LRC and SANDIA profiles. Of these, profiles NACA type are well known, and in some commonly used as practice for the validation of numerical methods.Heliciel provides free database of profiles with their polar of about 1,000 profiles of all kinds. To use it simply download on the interactive data base page héliciel
NACA-type profiles:The predecessor of NASA was the NACA (National Advisory Committee for Aeronautics). This organization has studied different families of profiles corresponding to various applications. Among the latter, we must distinguish the family of profiles in four digits, the five numbers and laminar NLF profiles with the designation in the documentation.
- .Family of profiles in four digits. In this family, we identify a profile by four digits, the first specifying the maximum camber relative percentage of the chord, the second indicates the position of the arch as a percentage of the chord and the last two digits representing the maximum relative thickness, always a percentage of the chord
- - 2 represents the maximum camber relative (2 %);
- - 4 represents the position of the maximum camber (40 %);
- - 15 represents the maximum relative thickness (15 %).
In Heliciel, performance of calculated or measured profiles are stored as database containing the CL (lift coefficient), Cd (drag coefficient), Cm (moment coefficient) relative to each angle of incidence, and each reynolds number, in which the profile was evaluated and normalized coordinates defining the geometrically ...Optimize the shape of the profiles
A system with a propeller or wing can have a more or less efficient. Whether in terms of finance or quality workmanship, materials and efforts for the realization of a project need to be offset by the quality of the result. The performance of our system is an implacable judge of our work! The optimum performance will be obtained only if we properly design our profiles propeller blade or wing. The main qualities for which a profile is selected is its lift / drag ratio and strength provided by its thickness. These two qualities are antagonistic they involve a compromise between strength and performance of our wing or propeller blade. HELICIEL automatically optimizes profiles by selecting their according to lift / drag ratio and maximum thickness distribution. But knowledge of the geometric parameters determining the lift / drag ratio profiles can be useful if you want to manually select your blade profiles or wing.
- : the lift / drag ratio represents the forces at play in the profile. Generate maximum lift with minimum drag is the key to the performance of our system. It is the ratio of the lift on the profile drag, or more precisely Finesse = Cl / Cd. A "good CL" is strong, and a good "Cd" is a low Cd.
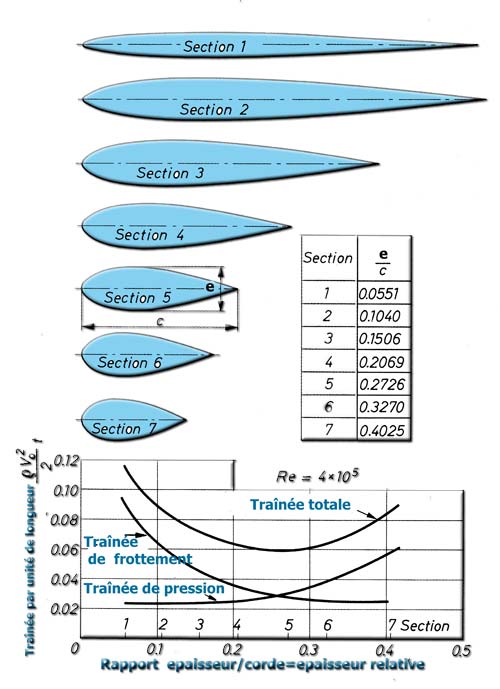
- 1 the Cd:The higher the relative thickness of the profile, the greater the Cx is important. To increase the lift / drag ratio, we can reduce the relative thickness. Particular attention is to focus on the composition of Cx: Drag is a primarily the result of two forces:
1 - the pressure forces whose coefficient Cxp is noted.
2 - and the friction forces whose coefficient is noted CXF.
Cx = Cxp + CXF.
For example compare the Cx of a sphere and an airship hull (the first flow regime) of the same volume: The observed distribution around the sphere pressure gives us the pressure drag therefore Cxp the sphere corresponds to the vector sum of pressures shown in this figure. The Cxp of the sphere is 0.511. For the sphere, Trails friction is relatively small compared to the pressure drag and you can write Cx = 0.511 = Cxp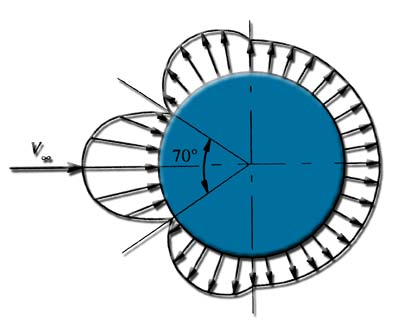
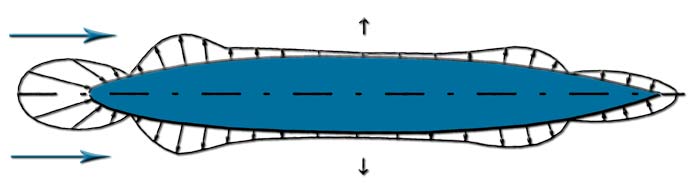
- The observed distribution of pressure around the hull airship gives us the pressure drag therefore Cxp the sphere which corresponds to the vector sum of pressures shown in this figure. The Cxp the hull is 0.0331. The trails are now greater friction due to the large surface area and the total drag measured gives us a Cx = 0.1 then aCXF = 0.1-0.0331 = 0.066
- 1 the Cd:The higher the relative thickness of the profile, the greater the Cx is important. To increase the lift / drag ratio, we can reduce the relative thickness. Particular attention is to focus on the composition of Cx: Drag is a primarily the result of two forces:
Here is an illustration of the dependence of the drag and the relative thickness of Marchag. Note that the pressure drag can become a minority on the low thickness, which implies that to optimize our wing at low thicknesses we must pay attention to the state of the surface which is heavily involved in the skin friction drag.:
- 2 The CL :We can also increase our lift / drag ratio and our performance system, by increasing the lift coefficient CL of our profile.
- The change of direction (correctly oriented) generates lift
- camber causes (with incidence) the change of direction that we ask the fluid therefore the lift.
- for high speeds the camber should remain low, and at low speeds, the camber can be strong.
So we see that the Cx is strongly influenced by the relative thickness of our profile. Now interest ourselves in the second parameter of lift / drag ratio.:
The camber of our profile is a key player in the lift. We would be tempted to say that the camber brings the lift but a major phenomenon disturbs this relationship camber lift: The stall ... The lift force is the variation of momentum of our fluid. The lift is the result of our ability to change direction to the fluid. The more we deviate the fluid down, the lift will be more important. Like a car in a curve, the greater the mass of fluid is faster, its inertia is important, and the less it will accept to change direction. The camber of our profile must respect this will of fluid to go straight, and ask only a change of direction that it can perform. If the curve is too abrupt, the fluid separates from the curve, and the effect of lift s' collapses! If the fluid is slow it will accept a sharp turn, so sudden camber. If the fluid is fast, the camber will be low to avoid stallwe will remember:
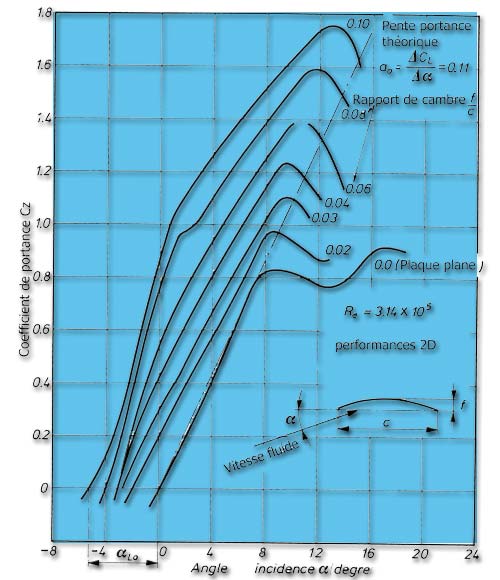
This graph of the evolution of the lift coefficient as a function of camber plates curved shows the increase in lift with camber:
Here is a graph showing the number of lift coefficients measured on three profiles (625 göttingen thick profile göttingen 417 sheet curve and flat plate) of different camber at different rates. Speed profile is given by the Reynolds number.
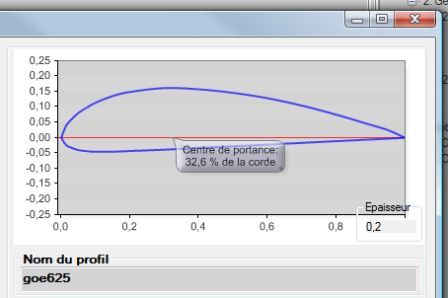
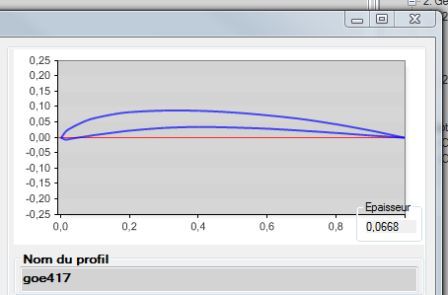
profil göttingen 625 et 417 (database heliciel)
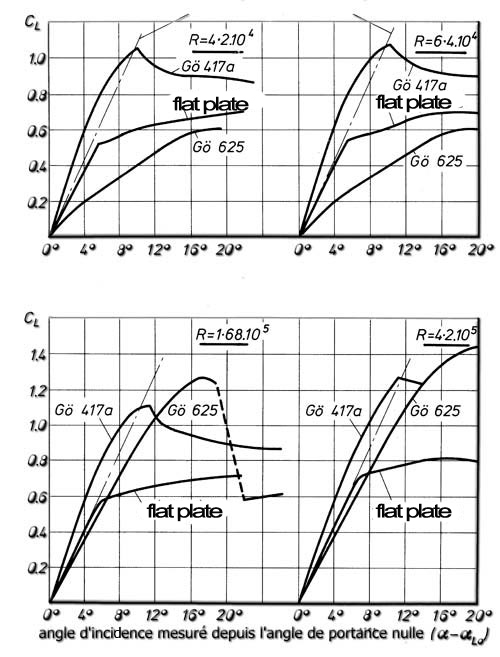
We have seen the impact of the camber profiles on the lift but it curves above show us that the curvature is not sufficient to predict the lift because the speed and thickness play a role difficult simply determine.

 Global site map
Global site map Mecaflux
Mecaflux Tutorials Mecaflux Pro3D
Tutorials Mecaflux Pro3D Tutorials Heliciel
Tutorials Heliciel Mecaflux Store
Mecaflux Store Compare software functions
Compare software functions Quotes, Orders, Payment Methods
Quotes, Orders, Payment Methods project technical studies
project technical studies