- The concept of momentum is key to understanding the functioning of the propellers..
- Principle of change of momentum is used in the theory of Froude applied to propellers or theory Froude applied to energy capture propellers..
momentum amount of movement
Understand and master the momentum amount of movement:
The amount of movement of an object is defined as the product of its mass by its speed. When two objects collide, the momentum of each varies, but the total momentum of the system remains constant, at least with good approximation.
The variation of the amount of motion of an object is closely related to forces acting thereon. For this reason, one can often determine the average forces involved in a complex phenomenon from changes in amount of movement. forces Related to changes in amount of movement involved in a quantity called the impulse.IMPULSE AND MOMENTUM
We will define impulse and amount of movement with an example. We then establish a relation between these two variables. the Fig. 7.1 shows a man pushing a cupboard. Let us assume that the frictional forces on the cabinet are negligible. We can establish, using Newton's laws, a relationship between the forces acting on the cabinet,the time during which the forces act and the speed variation of the cabinet.
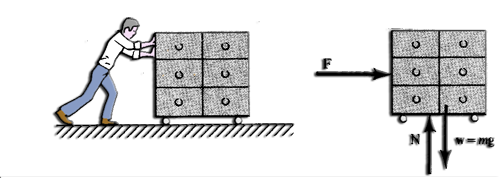
Assume that the force F is exerted on the rack cabinet during a time interval Dt. During this time interval, the speed of the cabinet varies from V0 to V2. By definition, the average acceleration, a, is equal to the variation in speed divided by the time interval: a = (V2- V0)/Dt. Newton's second law relates the average acceleration and the resultant force: F = m.a. We therefore:
- F= m. ( (V2-V1) /Dt )
- F.Dt= m.V2- m.V1
- impulsion=FDt
- P= mv
- F.Dt= P' - P
example
- We hit a stoped baseball. Immediately after the shot, the ball speed is 40m / s.
The initial momentum of the ball is zero since the ball is stopped.The final amount of movement is P' = m.V'. From the relation F.Dt= P' - P, we deduce that the average force F exerted on the ball is:
- F=(m.V2)/Dt =( (0,15 kg)x(40m/s))/0.001 = 6000 N.
CONSERVATION OF MOMENTUM:
Momentum is a very useful concept to study the interaction between two or more objects. Fig. below schematically a collision between two objects. Friction is assumed to be negligible. Each object is subjected to the force of gravity and a normal force.
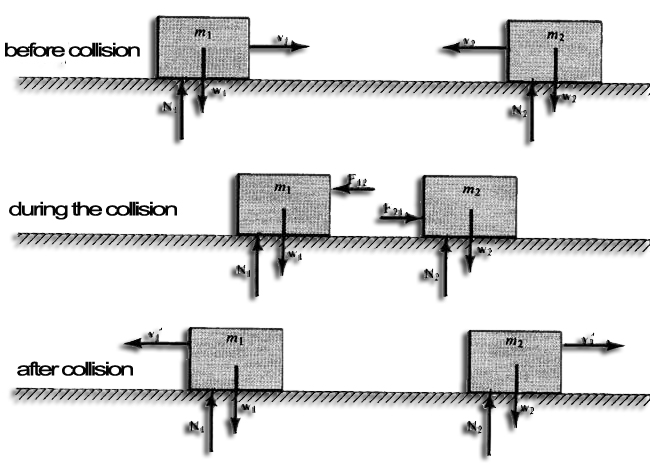 During the collision, as the objects exert forces on each other. These F 12 and F 21 forces are forces of action and reaction. So they have the same magnitude, but opposite directions.
During the collision, as the objects exert forces on each other. These F 12 and F 21 forces are forces of action and reaction. So they have the same magnitude, but opposite directions.
- therefore F 12 + F 21 = 0.
- for The object m 1 , F12. Dt = P'1- P1
- for The object m 2 , F 21. Dt = P'2 - P2
- P'1- P1 + P'2 - P2 =0
- P1+P2=P'1+P'2
- This example illustrates the result:
A cannon mounted on a railroad wagon. This wagon is initially at rest, but it can move without friction . cannon fires a bullet with a mass m = 5 kg and has, relative to the ground, a horizontal speed y = 15 m/ s. The ball moves towards the wall of the wagon.The total weight of the cannon and the wagon is M =15.000 kg. (a) What is the velocity V of the wagon when the ball is in flight? (b) If the ball encrusted in the wall of the wagon, what is the speed of the wagon and the ball after impact?
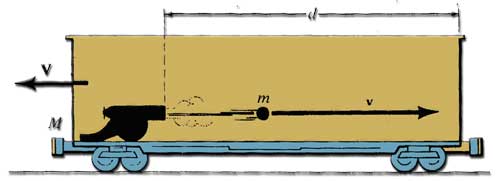
(a) At the fires, the cannon exerts on the ball a force directed to the right. The ball exerts a force equal but opposite on the cannon.The cannon and the wagon are therefore subject a recoil to the left. The total momentum is conserved since there is no external force friction. The momentum before the cannon fires is zero. Therefore, after the fires, the momentum of the ball, which is directed to the right must be equal in magnitude to the momentum of the cannon and of the wagon. laquelle est dirigée vers la gauche. which is directed to the left.We therefore
- mv = M.V et
- V=m.v/M=((5Kg) X (15m/s)) /15000Kg =0.005 m/s
(b) When the ball encrusted in the wall, it exerts a force on it. She is pointing to the right .In turn, the wall exerts a force on the ball, which is directed towards the left. The cannonball and the wagon then stop moving. At this time, the amount of movement, resulting is again zero. Meanwhile, the car was moved to the left and the cannonball to the right.

 Global site map
Global site map Mecaflux
Mecaflux Tutorials Mecaflux Pro3D
Tutorials Mecaflux Pro3D Tutorials Heliciel
Tutorials Heliciel Mecaflux Store
Mecaflux Store Compare software functions
Compare software functions Quotes, Orders, Payment Methods
Quotes, Orders, Payment Methods project technical studies
project technical studies