 Modeling a wing mast sail in heliciel
Introducing the mecaflux software suite:
Wings or foils modeling in heliciel
Aerial propeller modeling in heliciel
Boat propeller modeling in heliciel
Ventilation propeller modeling in heliciel
Wind turbine propeller modeling in heliciel
Tidal turbine modeling in heliciel
Kaplan propeller modeling in heliciel
Modeling a wing mast sail in heliciel
Introducing the mecaflux software suite:
Wings or foils modeling in heliciel
Aerial propeller modeling in heliciel
Boat propeller modeling in heliciel
Ventilation propeller modeling in heliciel
Wind turbine propeller modeling in heliciel
Tidal turbine modeling in heliciel
Kaplan propeller modeling in heliciel
Wing of finite span and downwash: Theory Prandtl lifting line
Understand and master the Wing of finite span and downwash: Theory Prandtl lifting line:
Vortex sheet and losses wingtip shown schematically in software Heliciel:
Rectangular wing length of 2 meters Aspect ratio = 4 ratio (Lift / Drag) =16 |
Rectangular wing length of 9 meters Aspect ratio = 18 ratio (Lift / Drag) =32 |
| Triangular wing length of 2 meters. Aspect ratio = 5 ratio (Lift / Drag) =19. | Triangular wing length of 9 meters. Aspect ratio = 33 ratio (Lift / Drag) =36 |
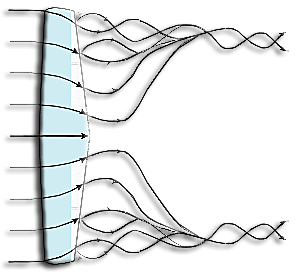
We have seen in the page for general information on the wings and hydrofoils that drag and lif forces calculated using the 2D CL and Cd are theoretical values, not taking into account the vortex phenomena. These vortex phenomena are caused by the pressure difference between the upper and lower surfaces of the wing:



Change of the effective angle generated by the induced down speed in the profile of an element:
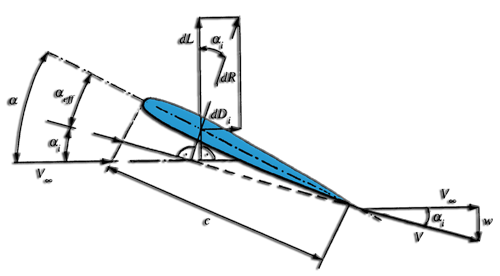
- The infinite speed V is the velocity at the inlet at a distance considered to be infinite, so undisturbed by the wing.
- Velocity w is the velocity induced by the vortices. Induced velocity is downward, so it is negative.
- The angle a is the geometric angle of incidence.
- Angle ai is the angle of incidence induced.
- Angle aeff is the angle of incidence really seen by the profile.
Lifting line Prandt's ltheory Ludwig Prandtl has developed the first method for the analysis of a wing of finite span in 1918 equating all vortex filaments attached to a wing has a single filament called "lifting line." Laws and theorems defining vortices allow calculation of induced velocities:
- The law of Kutta-Zhukovsky gives us the relationship between the lift force (Newtons) and the intensity of the vortex attached (Γ) on a wing length L (m), immersed in a fluid flow velocity V (m / sec), and density r(kg/m3):
- Lift = Γ. r . Vinf. L
- Γ= Lift / (r . Vinf. L)
to recall the formula for the lift:
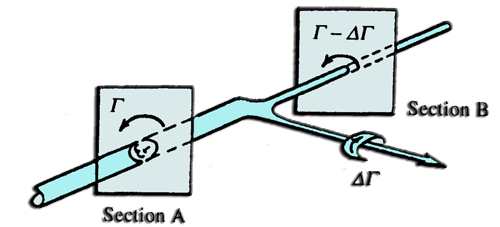
- According to theorem Helmotz a vortex must be closed, and can not finish in the fluid, this implies that the lift of an element, creates a vortex of constant intensity (Γ), distributed along a line, which forms a closed loop..

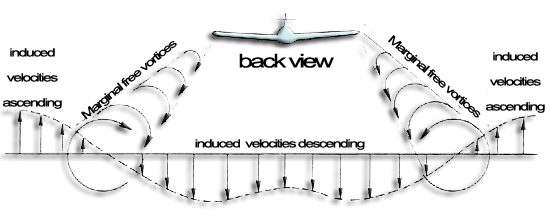
In reality, when the wing is flying, the "vortex departure to downstream infinity" is far enough away from the wing to overlook the induced velocities, it causes on the wing. (because the velocity induced by a vortex varies as the inverse of the distance to the axis of the vortex). So we consider only the free vortices marginal, and induced download speeds, as seen by the wing. Free vortices marginal are defined as semi-infinite, because it starts at the end of the element, and extend to the downstream infinity.
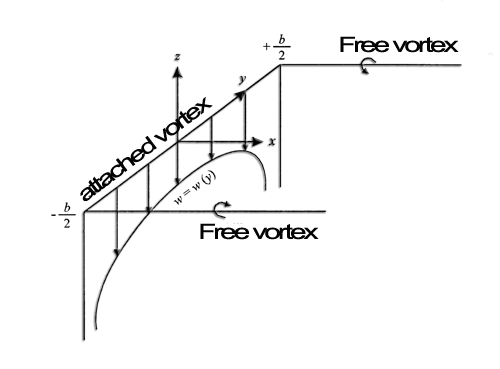
- By replacing the lift force by a line vortex attached at the center of lift profiles (about 1/4 of the chord) which are extended by two vortices, intensity (Γ) constant , and neglecting the vortex departure, we obtain a horseshoe vortex system::

- The Biot-Savart law gives us the induced velocity w(m/sec) at a point (P) located at a distance h of a tip vortex of intensity (Γ)semi-infinite because it starts at the end of the element and extends to downstream infinity.The lift of the element (known from the profile CL) giving us the intensity , It is therefore possible to determine the speed-induced w, to the point P:
At point P, the induced velocity is: w= - Γ/(4.pi.h) .w is negative because downwardly
- Expression of induced velocities for a single isolated vortex system:
Let the point P in the system of two horseshoe vortices, where the induced velocity is produced by two free vortices. Point A is located at -b/2 and +b/2 and the point P on the Y axis.Induced speed based the y-position is composed of two terms:
- terms - Γ/[4p(b/2+y)]representing the contribution of vortices located at point A with y=-b/2
- terms - Γ/[4p(b/2-y)] representing the contribution of vortices located at point A with y=b/2
Giving the expression of the induced velocity, depending on the position y for a single vortex system:
In this latest expression of the induced velocities for a single isolated vortex system, when the position y approach to tip (y=b/2 ou y=-b/2), induced velocity tends to negative infinity. Which can not correspond to a realistic representation of the wing of finite span. to remedy this, Prandtl, introduces the concept of lifting line:
- w(y) = -Γ/[4p(b/2+y)] - Γ/[4p(b/2+y)]
- equivalent to :w(y) = - Γ/(4p) .{b/[(b/2)²-y²]}
- Expression of induced velocities for a set of vortex systems: The lifting line
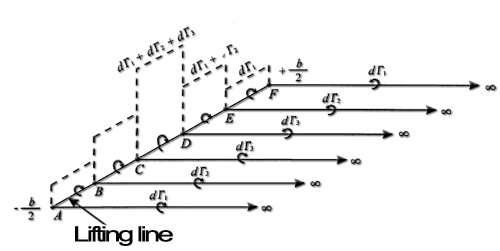
The first theorem Helmotz defining the laws of vortex motion states that the intensity (Γ) of an isolated vortex is constant and equivalent to the lift. A variation of the lift (therefore the intensity Γ) can not be represented by a vortex system isolated.Variation of lift, therefore the vortex intensity, on a wing:

A system of vortices superimposed is used to represent the variation of 'vortex intensity associée associated with the lift of a wing. At each point of the wing, in which is a variation of lift, a vortex of intensity equal to the change in lift is formed:
In reality this vortices sheet forming on the trailing edges is combined ,to form the two vortices sometimes visible:
But the variation of lift and intensity is continuous and progressive on the wing, the number of horseshoe vortices, intensity dΓ superimposed on the lifting line describing the intensity variation is infinite.
- Elementary dG intensity of horseshoe vortex, corresponding to the lifting line segment [dy] positioned at y on the figure above, is given by : dΓ= (deltaΓ/delta y).dy
- the free vortex intensity dΓ will induce dw velocity at the point y0:
using the law of Biot savart defining the velocity induced by a semi-infinite vortex:

where is substituted :
- Γ by (deltaΓ/delta y).dy, and h by y0-y
we obtain the elementary induced velocity at the point y0, produced by free vortex intensity dΓ, passing through y :
- dw= - {(deltaΓ/delta y).dy}/{4p.(y0-y)}
The total speed y0, induced by integrality of free vortex layer from -b/2 to b/2 is:
- w(y0) = -1/(4p) ∫(- +b/2) {(deltaΓ/delta y)/(y0-y)}.dy

( references:"Aérodynamique subsonique" Ion Parashivoiu école polytechnique de Montréal .
- ai(y0)= atan[-w(y0) / V∞]
You will also find a description of the theory of Prandtl lifting line on the site: http://j.haertig.free.fr/aerodyn_theorique/index.html eand in particular this document pdf :Theory of Prandtl lifting line


 Global site map
Global site map Mecaflux
Mecaflux Tutorials Mecaflux Pro3D
Tutorials Mecaflux Pro3D Tutorials Heliciel
Tutorials Heliciel Mecaflux Store
Mecaflux Store Compare software functions
Compare software functions Quotes, Orders, Payment Methods
Quotes, Orders, Payment Methods project technical studies
project technical studies