- To understand Theory Froude, the notion of momentum must be mastered, because it is on the balance of momentum that the Froude theory is based ..
Froude approach allows us to assess the axial induced velocity using a control volume around the fluid stream passing through the
propeller. By calculating the volume of fluid, which must penetrate the volume control laterally,due to the contraction of the fluid stream caused by the increase in velocity produced by the propeller: Following the approach proposed by Froude, we can consider the propeller as a uniformly charged disk with an infinite number of blades (Fig. 1). In addition, we set the following assumptions:
- are not taken into account the rotation of the flow.
- we consider a fluid stream out of which the flow is not disturbed
- The pressure at infinity upstream and downstream is equal to the static pressure of undisturbed flow
- The air disturbance are sufficiently small that it is assumed that the fluid density is constant.
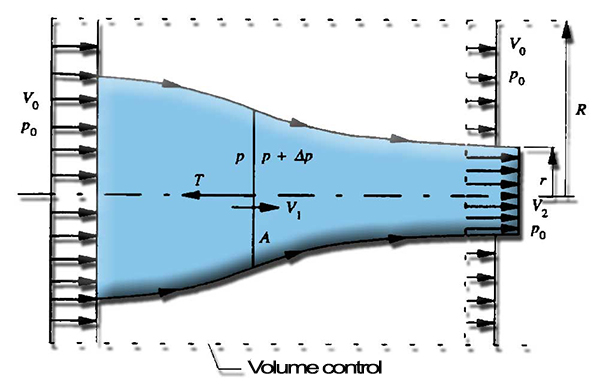 fig. 1
fig. 1
lthe
continuity equation allows us to calculate the volume added to the control zone per second (volume flow Q in m3/sec),:
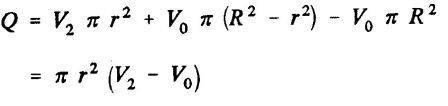
Q is the volumetric flow discharged from the volume control. From the
theorem of momentum, the thrust, T of the propeller is obtained, that is to say the variation of the amount of movement between the sections 2 and O, whose projection on the horizontal axis indicates thrust :
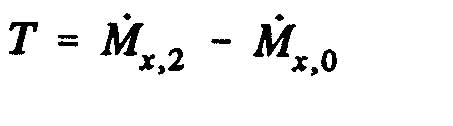
The derivative of the momentum versus time :
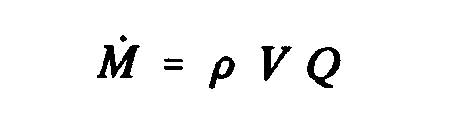
Momentum out "M_2" volume control in Section 2 =
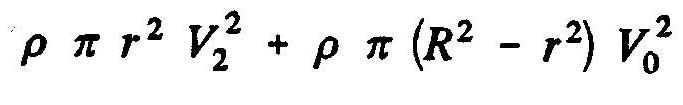
Total amount of movement "M_1" within the volume control = Momentum in the volume entry - momentum laterally inserted=
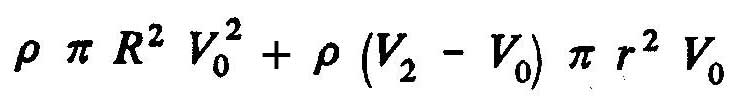
Therefore, the axial force of the fluid on the rotor becomes(T=M_2-M_1):
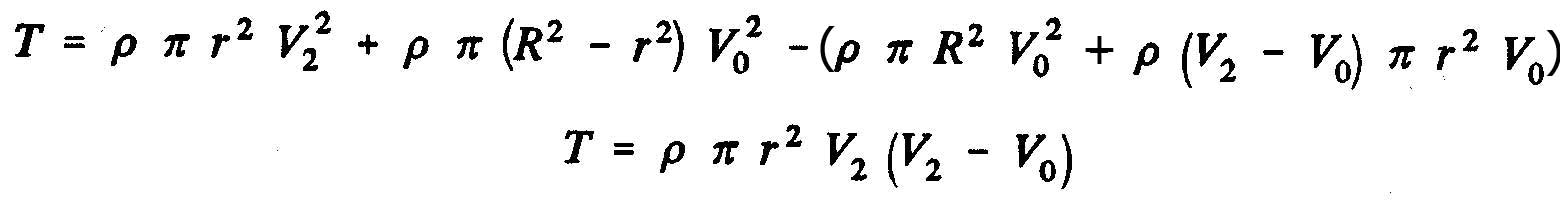
One can also express the axial force of the fluid on the rotor T, according the result of the static pressure which is exerted on the surface of dis:
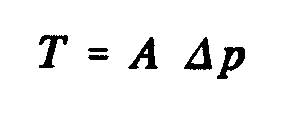
where A is the surface of the disc swept by the propeller and Dp, the pressure difference across the disc. Using
Bernoulli's equation, we obtain
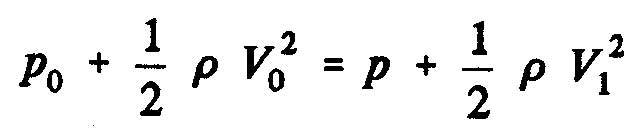
pressure difference O to 1 upstream, and:
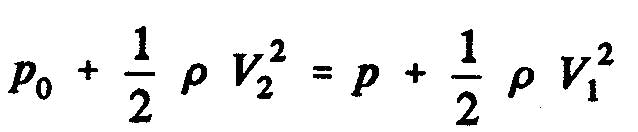
pressure difference 2 to 1 downstream.
The static pressure difference between the upstream and downstream sides of the disk of the propeller as the expression:
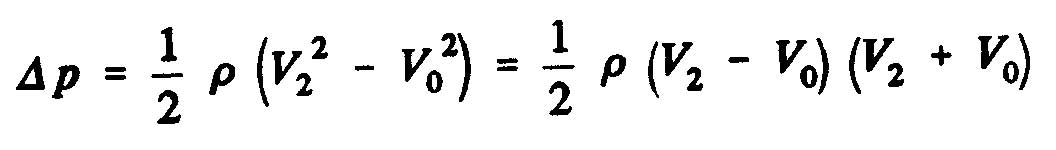
From the continuity equation:
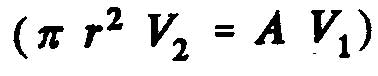 ,
, can be derived:
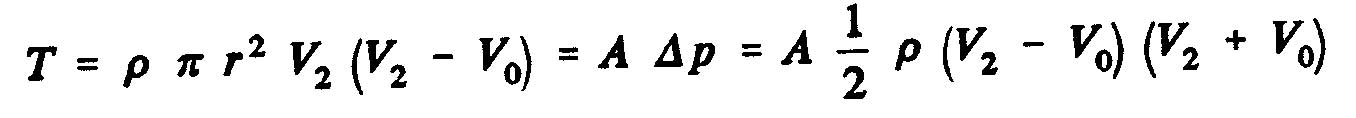
and consider the speed of the flow through the disk as an arithmetic average of the velocities upstream and downstream of the propeller:
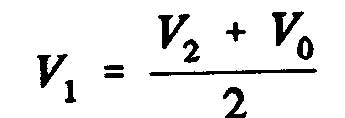
Is called induced velocity w, increasing speed at the propeller disk:
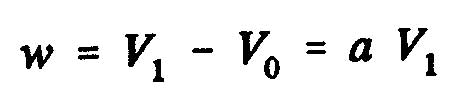
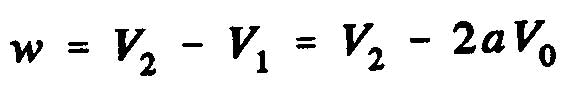
where "a" represents the axial interference factor.
Now, if we consider the expression:
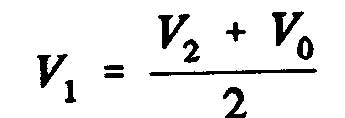
,the axial force exerted on the disc of the impeller is:
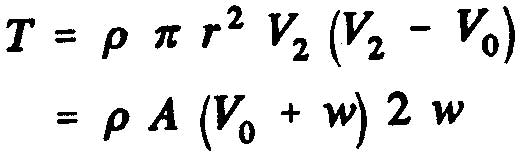
From this expression we can identify push the notion of mass flow: The mass of fluid passing through the propeller per second :
So we see that the thrust of the propeller is: T=m.(v2-v0)
- It is important to note that create thrust, therefore, is to increased the speed of a mass flow of fuide. This highlights the levers available to us to generate the propulsive force: The choice to act on the mass or speed variation is crucial for the propulsive efficiency
The theory froude gives us the axial induced velocity. It will be linked to the
theory of the blade element to give a decomposition of the induced velocity in tangential and axial induced velocities necessary for the prediction of the incidence angles and the geometry of the blades..
Bibliographic references propeller
 fig. 1
fig. 1 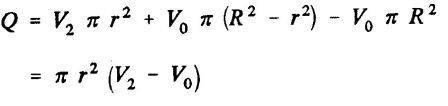
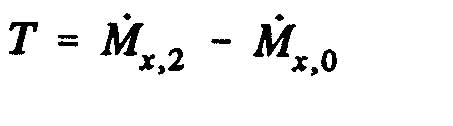
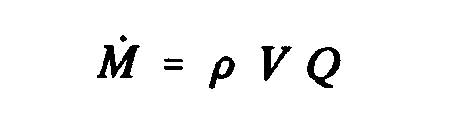
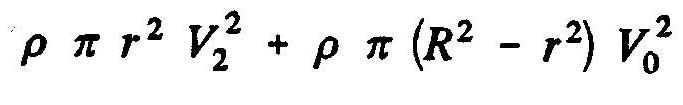
![]()
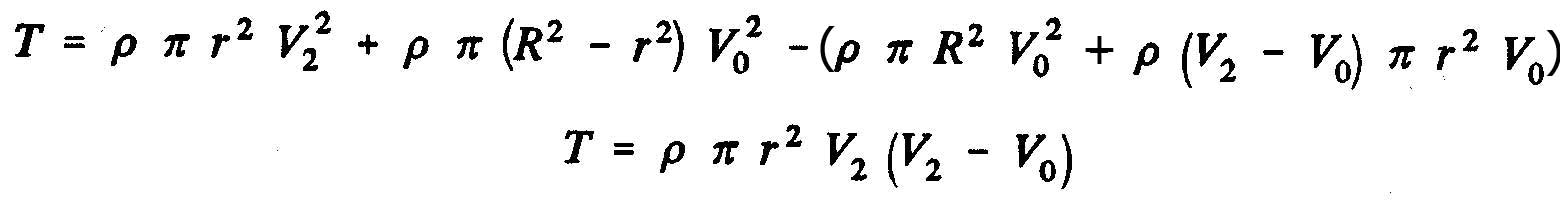
![]()
![]()
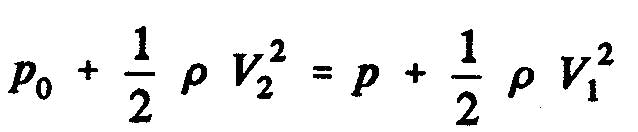
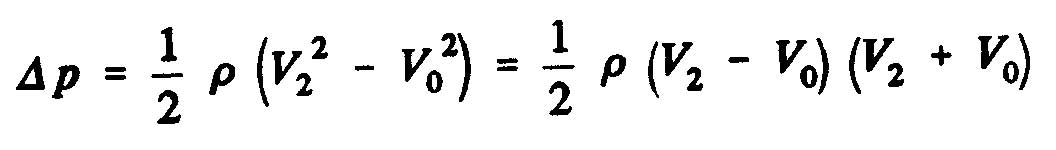
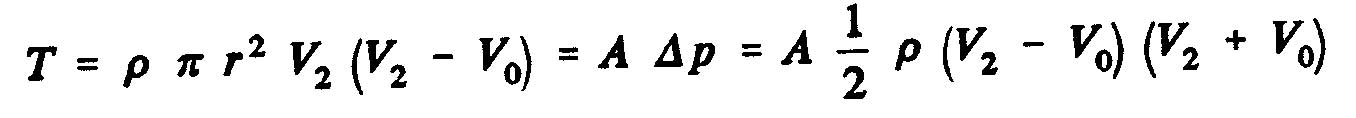
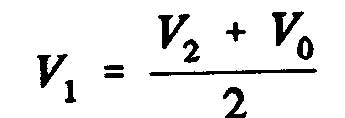
![]()
![]()
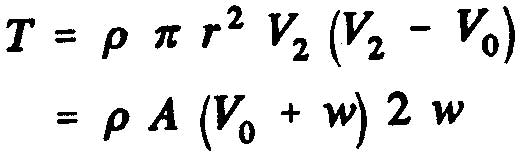

 Global site map
Global site map Mecaflux
Mecaflux Tutorials Mecaflux Pro3D
Tutorials Mecaflux Pro3D Tutorials Heliciel
Tutorials Heliciel Mecaflux Store
Mecaflux Store Compare software functions
Compare software functions Quotes, Orders, Payment Methods
Quotes, Orders, Payment Methods project technical studies
project technical studies