hydrodynamic resistance of ship hulls

Understand and master the hydrodynamic resistance of ship hulls:
The study of the forces of resistance on a boat hull shape allows to evaluate the propulsive force that will serve to advance to the desired speed. The force resistance to forward (expressed in Newtons) is opposed to the ship. This force may be measured by towing the vessel. Propulsive force equal and opposite will be provided by the propulsion machinery to maintain the speed of the ship. As it is not possible to tow a ship that is not yet built, this it is necessary to formulate a practical and accessible method giving the designer and shipbuilder concrete design elements of the propulsion machinery.It is convenient to decompose the total hydrodynamic force resistance (Rh), distinguishing three main resistances causing the total resistance:
- Viscous resistance (Rv) composed of
- Frictional resistance dependent on the wetted surface and roughness .
- resistance pressure dependent on the hull shape and swirls it generates
- La résistance de vagues (Rw) dépendant de la vitesse et de la longueur du navire..
- The aerodynamic resistance (Ra) superstructures exposed to the wind (which will be considered here as negligible)
There is a relationship between the length and between two crests of a wave (L meters) and velocity (V m / sec) given by::
- V/√(9.81 X L)=0.4
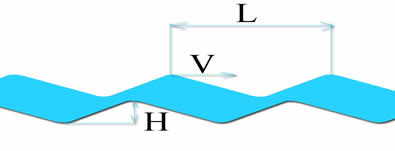
:Incidentally, as it is possible to determine the energy contained in a wave by the equation: E (joules) = (1/8) x density (kg/m3) x 9.81 x H ² x L, we could estimate energy absorbed by the waves observed..
- The waves created by the ship have the same speed as him, so it is possible to determine the relation: L = (2Pi /9.81) x V² the distance between two crests of the waves produced by the boat Replacing V by speed boat..
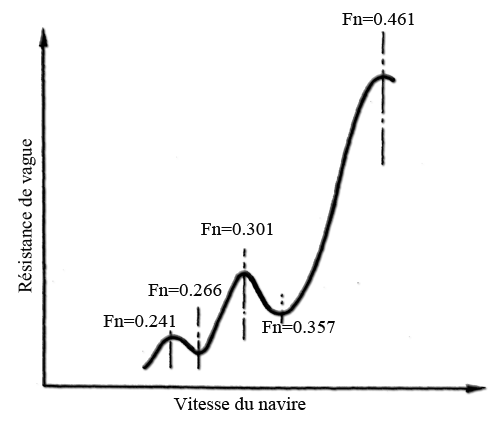
- Substituting in the relation V/√(9.81 X L)=0.4 , The wave length of by the waterline length Lf, Froude deduce the significant number of wave effects on the resistance to the advancement of ships, and the formula: C/√(9.81 X Lf) designated the Froude number with C = speed of the boat and Lf = waterline length. Froude number Fn allows us to assess the shape of the waves accompanying the ship. Evaluation of the wave regime and evolution of specific resistance as a function of Froude number:
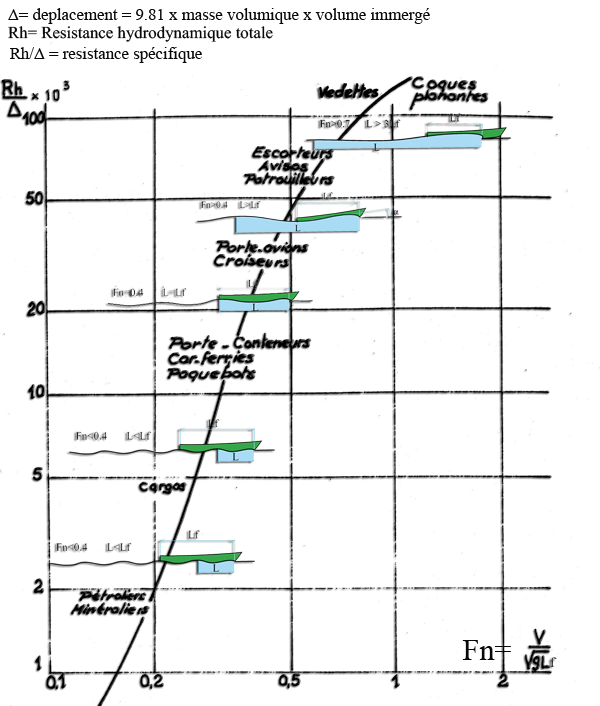
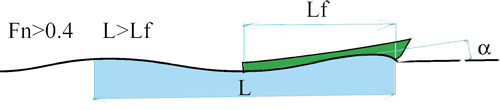
Froude number less than 0.4:
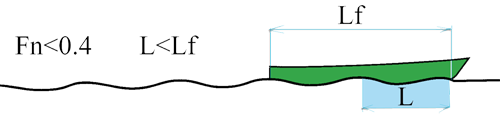
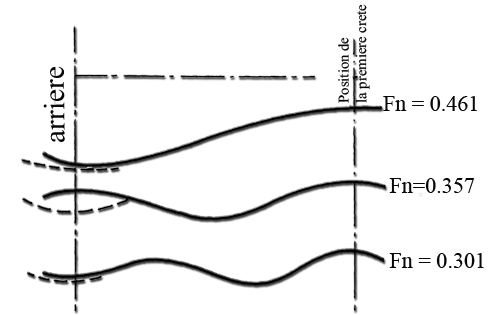
- At low Froude number (lower is 0.26) 3 ridges low height at least along the boat. The wave resistance is low and the resistance of friction represents 70 to 90% of the resistance to advancement. Above 0.26 resistance wave increases and the interaction between the Bow wave and the wave occurs REAR to significant way on the resistance to advancement by the effect of adding or subtracting the height of ridges. See in more detail the interaction:
The ship generates mainly two wave trains :
- Waves emerging in the Bow and with a maximum height of the first peak is a 1/4 of the length L
- Waves created by sucking the rear of the boat, emerging at the back of the boat and starting with a hollow
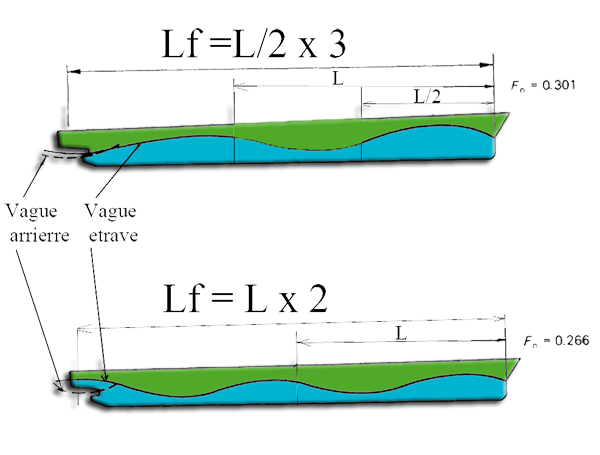
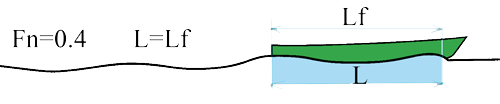
- If Lf is a multiple of L on a crest of wave Bow which overlaps and cancels the hollow of the emerging system at the rear.'s Resistance to the advancement through a minimum
- If Lf is odd multiple of L / 2 (eg Lf X1 = L / 2 or 3 x Lf = L / 2), then the wave outcome of the Bow present a hollow at the rear of the ship that combines with wave REAR and resistance to the advancement through a maximum.
These values correspond to a remarkable series of Froude number:That we can place on a curve of wave resistance:
Froude number = 0.4:
Froude number > 0.4 :
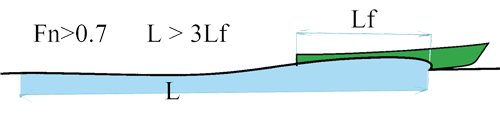
Froude number > 0.5:
Overall methodology for calculating resistance to the advancement of hulls.Consider a plane and infinite calm water. We neglect the aerodynamic resistance. Method of calculationl:
- Calculation of the wet surface
- Calculating the ship displacement
- Calculating the number of froude
- Estimated wave regime
- Estimating the angle of camber of the vessel
- Estimated residual drag by the method of Savitsky
- Calculation of the viscous resistance: calculating the frictional resistance + resistance calculation pressure (form)

 Global site map
Global site map Mecaflux
Mecaflux Tutorials Mecaflux Pro3D
Tutorials Mecaflux Pro3D Tutorials Heliciel
Tutorials Heliciel Mecaflux Store
Mecaflux Store Compare software functions
Compare software functions Quotes, Orders, Payment Methods
Quotes, Orders, Payment Methods project technical studies
project technical studies