La Theorie de Froude relative aux hélices de captage "axial momentum théory" , nous a permis de faire la relation entre la vitesse lnduite axiale et la force de poussée.Cette théorie suppose que l’écoulement ne subit aucun mouvement de rotation et ne nous donne aucune indication sur la forme a donner à notre pale.

En réalité, la loi de conservation du moment cinétique, impose que l’air doit avoir un mouvement rotatif afin que le rotor puisse extraire un couple utile. Dans ce cas, le sens de rotation de l’écoulement de l’air est opposé à celui du rotor.

La théorie de l'élément de pale couplée à l' axiale momentum théory, s'appuie sur les résultats de la théorie de froude pour estimer la force axiale élémentaire (relative à un élément), et introduit les performances des profils répartit par éléments le long de la pale. L’introduction du mouvement de rotation de l’air permet à ce modèle de mieux approcher la réalité et d’obtenir les vitesses induites tangentielles et axiales composant la vitesse induite amenée par la théorie de froude utilisant la variation de quantité de mouvement, donc des résultats plus fiables. L'introduction des performances Cx et Cz des profils permet de déterminer la géométrie de la pale, donc de construire concrètement une pale.

La théorie de l'élément de pale nous permetra de définir un facteur d'induction axial a et un facteur d'induction tengentielle a' .La resolution d'un syteme d'équation par itérations convergeantes introduisant les performances sous forme de Cx et Cz des élément de pale nous permetra d'obtenir les vitesses induites et donc les performances des éléments.

Nous verrons aussi 2 corrections, une corrigeant le fait que le nombre de pale est considéré comme infini dans la methode de froude(facteur de perte de bout de pale de Prandtl), et l'autre corrigeant les resultats pour les fortes valeur d'induction axiale ou la theorie de froude n'est plus valide(correction de Glauert pour les facteurs d'induction axiale supérieures a 0.4)

 

Dans l’élaboration de ce modèle, les suppositions suivantes sont envisagées

• L’écoulement en amont loin du plan du rotor, est complètement axial.
• Au niveau du plan du rotor, la vitesse angulaire de rotation de l’air est ω, cette vitesse diminue considérablement loin du rotor, en aval, de telle manière que la pression statique à cet endroit peut être considérée égale à la pression atmosphérique.
• Il n’y a pas d’interférence entre les éléments adjacents de la pale.
• L’écoulement de l’air autour d’un élément de la pale est considéré comme bidimensionnel.
  

 

dans la methode de Froude ,nous avons utilisé les variations de quantité de mouvement dans un volume de controle global, ici nous utiliserons des éléments annulaires comme volumes de controle pour connaitre la variation de quantité de mouvement élémentaire pour chaque anneau du rotor. La somme des performances de ces anneaux nous donnera les performances globales de l'hélice.

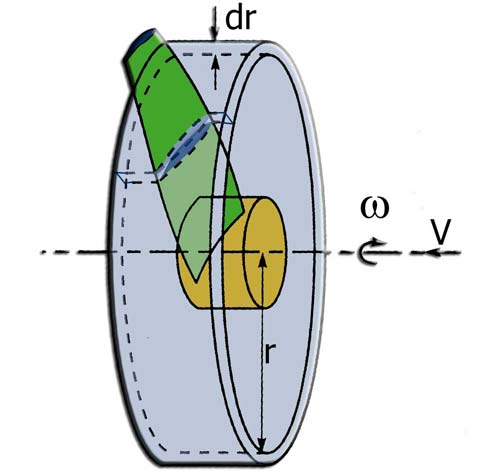
figure1

La variation de quantité de mouvement pour un élément d'epaisseur dr positionné au rayon r nous donnera donc la force de Traction T axiale sur l'élément :

avec vitesse en aval =u1 = V0.(1-a)

avec a facteur d'induction axial

La variation de quantité de mouvement pour un élément d'epaisseur dr positionné au rayon r nous donnera le couple MR sur l'élément en introduisant la vitesse induite tangentielle:

avec vitesse tangentielle C0 aval

C0=2a'wr (en considerant que la vitesse tangentielle en amont est nulle)

avec a' facteur d'induction tangentielle

avec r etant la distance a l'axe(metres) et w la vitesse angulaire (rad/sec)

en introduisant dans les équations 6.1 et 6.2 les facteurs d'inductions axiales et tangentielles a et a' décrit cidessus nous obtenons:

et

Rappelons que

la vitesse élément Ve(m/sec) perçue par un élément est la combinaison de la vitesse tangentielle Omega .r . (1+a') , et de la vitesse axiale V .(1-a)

La vitesse induite tangentielle est Wt(m/sec)= Omega .r.a'

La vitesse induite axiale est Wa(m/sec)= V .(-a)

Beta(radians) est l'angle de callage entre le plan de rotation et la corde du profil.

phi(radians) est l'angle formé par la vitesse de rotation omega.r et la vitesse en amont de la pale V

Phi+Alphai(radians) est l'angle entre le plan de rotation de l' hélice en la vitesse relative Ve.

Alpha(radians) est l'angle d'incidence percu par le profil. Alpha = (Phi+Alphai) - beta

nous constatons que:

 

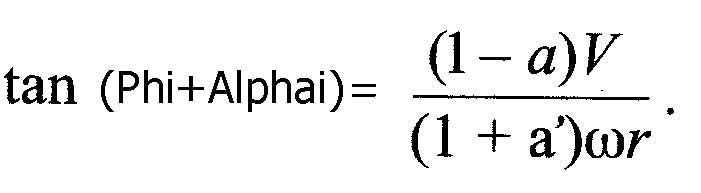
figure2

 

Rappellons encore que la portance dL est perpendiculaire à la vitesse élément Ve et à la trainée dD

Si les coefficients de portance et de trainée sont connus la trainée et la portance seront definies par

Portance dL(newtons) = 0,5. r. Ve². c .Cl

Trainée dD(newtons) = 0,5.r. Ve². c .Cd

avec Cl =coefficient de portance(Cz dans la litterature francaise) extrait de base de données,

Cd= coefficient de trainée(Cx dans la litterature francaise) extrait de base de données ,

c(metres) =corde du profil(distance entre le bord d'attaque et le bord de fuite).

Comme nous somme interessés par la force générant de la rotation donc parralele au plan de rotation et la force de poussée donc perpendiculaire au plan de rotation, la trainée et la portance seront projetées dans ces deux directions.

Force de rotation(newtons) Pn = dL. cos (Phi+Alphai) + dD. sin (Phi+Alphai)

Force de traction(newtons) Pt = dL. sin (Phi+Alphai) + dD. cos (Phi+Alphai)

ceci peut etre normalisé en respectant 0,5.r. Ve². c

comme:

Cn = CL. cos (Phi+Alphai) + CD. sin (Phi+Alphai)

Ct = CL. sin (Phi+Alphai) + CD. cos (Phi+Alphai)

donc

Cn = Pn/(0,5.r. Ve². c) ( 6.14 )

Ct = Pt /(0,5.r. Ve². c) ( 6.15 )

nous pouvons voir sur la figure 2 que

Ve. sin (Phi+Alphai) =V(1-a)( 6.16 )

et que

Ve cos (Phi+Alphai) =wr(1+a')( 6.17 )

La solidité s est definie comme la part de la surface annulaire de rayon r du volume de controle qui est recouverte par les pales de l'hélice.Cette solidité est calculée d'apres:

s(r)= (c(r)B)/(2p r ) ( 6.18 )

avec B le nombre de pale et c(r) la corde local et r la position radial du volume de controle.

Comme Pn et Pt sont des forces par unité de longueur, la traction ou poussée T et le couple MR sur le volume de controle d'epaisseur dr est:

Poussée sur élément(newtons): T=B.Pn.dr ( 6.19 )

Couple sur élément(newtons):MR=r.B.Pt.dr ( 6.20)

En utilisant l'équation (6.14) pour Pn et l'équation (6.16) pour Ve, l'équation (6.19) devient:

En utilisant l'équation (6.15) pour Pn et l'équation (6.16)et (6.17)pour Ve, l'équation (6.20) devient:

 

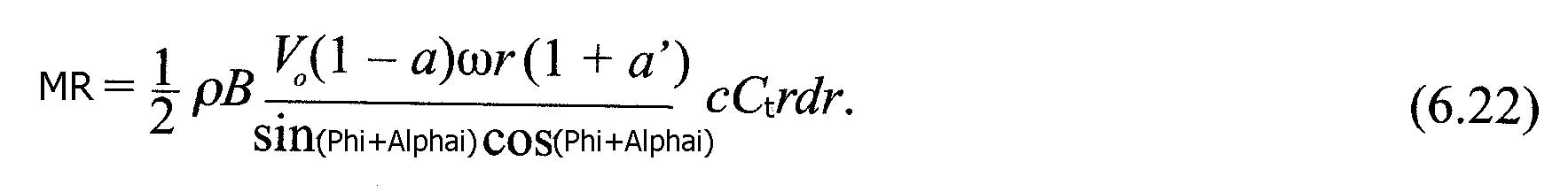
Si les deux équations (6.21) et (6.4) sont égalisées et que la définition de la solidité est appliquée,

nous obtenons l'expression du facteur d'induction axiale a:

et si nous égalisons les équations (6.22) et (6.25) nous obtenons le facteur l'equation du facteur d'induction tengentielle a':

Correction du nombre de pale

La méthode de froude considere une infinité de pale sur le disque rotor, Le facteur de correction de pertes en bout de pale dérivé par Prandtl est utilisé pour corriger les performances en fonction du nombre de pale.

Le fateur F est utilisé pour corriger les équations (6.4) et (6.5),elle deviennent donc respectivement:

et

Avec F facteur de perte en bout de pale de Prandtl calculé comme suit:

 

ou

Bétant le nombre de pales,R le rayon en bout de pale,r le rayon local de l'élément et (Phi+ Alphai) l'angle de fluide percu par l'élément.(voir figure 2)

En utilisant les équations (6.31) et (6.32), à la place des équations (6.4) et (6.5), pour etablir les équations des facteurs d'induction axiale a et tengentielle a', nous obtenons:

et

 

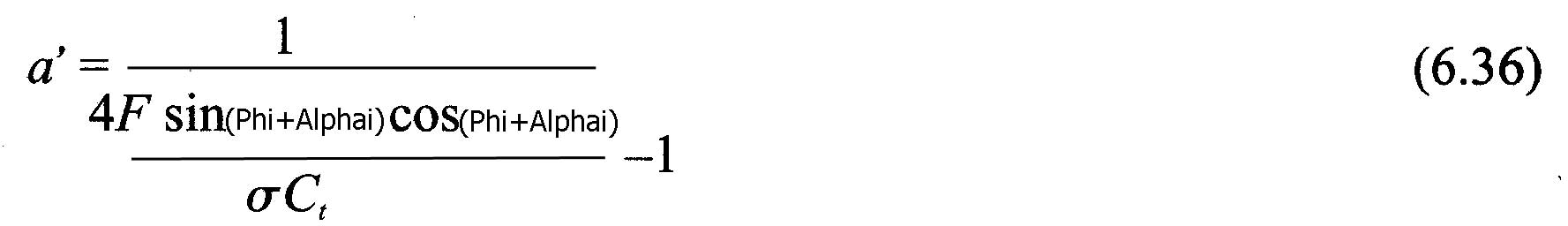
Correction des fortes valeurs d'induction axiale :

Lorsque le facteur d'induction axiale dépasse environ 0.4 , la theorie des variation de quatité de mouvement de froude n'est plus valide. Glauert propose des corrections en relation avec le coefficient de poussée. Plusieurs relations empiriques entre le coefficient de poussée Ct, et le facteur d'induction axiale, ont été établies pour correspondre aux mesures expérimentales.

Nous retiendrons celle trouvé dans Spera(1994) ou ac est approximativement 0.2.:

Le facteur de perte en bout de pale F est utilisé pour corriger la supposition du nombre infini de pales.

 

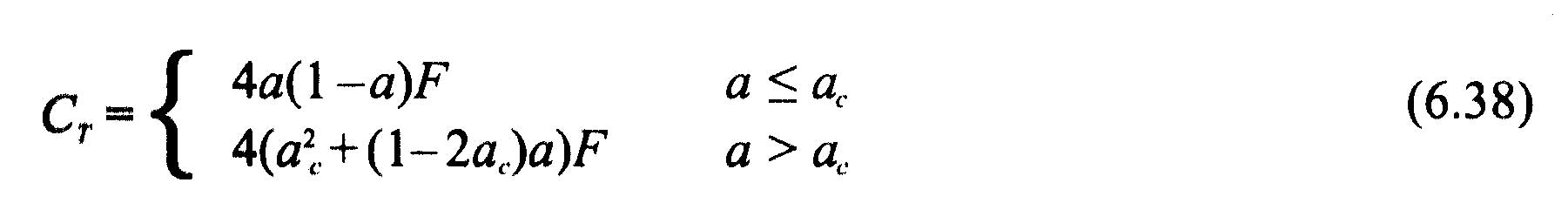
La poussée sur un élément est donnée par:

Le coefficient de poussée Ct est par définition:

Si l'équation (6.21) donnant T est introduite dans (6.39) nous obtenons pour Ct:

Nous pouvons donc maintenant introduire notre correction décrite par l'équation (6.38) :

Si a <ac:

ce qui donne :

(ce qui ne change donc pas notre équation (6.35) mais si:

a>ac:

cela nous donne:

Avec:

 

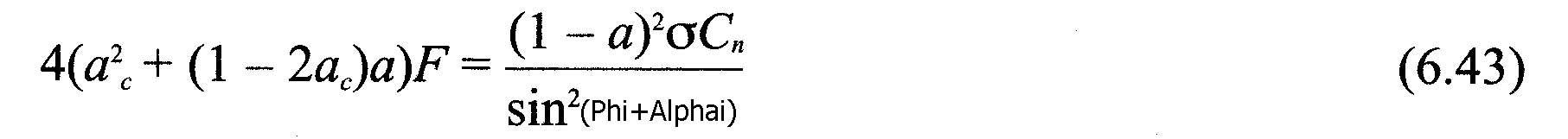
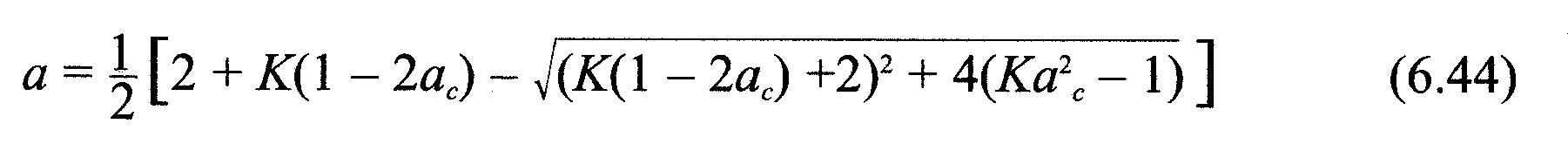
Les relations établies dans cette page nous permettent de créer un algorithme de calcul convergeant par itérations. Il est ainsi possible de calculer séparément les vitesses induites integrant les corrections de Prandtl et Glauert pour chaque élément de pale.Cette methode utilise les données de performances des profils. Elle permet de calculer la poussée et couple sur chaque éléments.En sommant ces résultats, les performances de chaque pales seront trouvées et la somme des résutats de chaque pale nous donnera les performances globales de notre Hélice. HELICIEL utilise en partie cette méthode reliée à la base de données de performances de profils interactive pour le calcul des hélices de captage d'énergie.

Algoritme de calcul :

1. initialiser a et a' ,a=a'=0.
2. caculer l'angle (Phi +Alpha i) en utilisant l'équation (6.7)
3. calculer l'angle d'incidence (Alpha) en utilsant l'equation (6.6)
4. importer les données de performances de la base de données pour l'angle alpha et le profil de 'élément
5. caculer Ct et Cn d'apres les équations (6.12) et( 6.13)
6. calculer a et a' d'apres les équations (6.44) ou (6.42)et (6.36)
7. si a et a' on changé de plus d'une certaine tolérence, retourner en 2 sinon terminer
8. calculer les forces sur les éléments

 

 

References bibliographique helice

 

statistiques

 

Logiciel:Heliciel